Regulación de genes - EBCP Latam 2025

Diseño de circuitos biológicos

El fenótipo de una célula puede considerarse como una función biológica que relaciona las entradas moleculares con un resultado celular concreto, como las proliferación, la apoptosis o la diferenciación. Como biólogos sintéticos, buscamos replicar ese mapeo de entrada-salida o reconfigurarlo para dar un nuevo fenotipo a la célula. Para lograrlo utilizamos circuitos biológicos: conjuntos de especies químicas (ácidos nucleicos, proteínas, metabolitos, etc.) cuyas interacciones transforman las entradas moleculares en salidas definidas, del mismo modo que las funciones matemáticas transforman variables en resultados.

Así como ocurre en ingeniería, a menudo existen múltiples formas de diseñar un circuito para resolver un problema determinado. En este workshop, exploraremos distintas arquitecturas de circuitos desde una perspectiva de diseño, con el objetivo de comprender los compromisos y ventajas entre las distintas alternativas y de identificar principios de diseño que expliquen por qué una solución puede ser preferible a otra. Derivar estos principios de forma empírica requeriría demasiado tiempo y esfuerzo, ya que depende en gran medida del método de prueba y error. En su lugar, recurriremos a modelos matemáticos para representar las interacciones clave entre las partes de un circuito biológico y así determinar las condiciones bajo las cuales dicho circuito funciona como se espera.

La lógica detrás de las ecuaciones de velocidad de reacción

El marco matemático que utilizamos se llama ecuaciones de velocidad de reacción, y nos ayuda a monitorear cómo cambian las concentraciones de las especies químicas en un circuito biológico a lo largo del tiempo (ver Technical Note #1). Una buena forma de comenzar con el modelado matemático es dibujar el circuito, asegurándonos de incluir todas las interacciones que nos interesan. Empecemos con las reacciones básicas presentes en prácticamente todos los circuitos biológicos: transcripción (TX) y traducción (TL). Imaginemos que tenemos un gen llamado $Y$ que se transcribe en una molécula de ARNm (ARN mensajero), a la que llamaremos $M_y$, y luego se traduce en una proteína, también llamada $Y$. Estos pasos aumentan las concentraciones de $M_y$ y $Y$, por lo que podemos considerarlos efectos positivos. Por otro lado, tanto $M_y$ como $Y$ se degradan, ya sea por descomposición natural o por dilución durante la división celular, lo cual podemos interpretar como un efecto negativo. Ahora vamos a representar todos estos eventos en un diagrama (Figura 1, izquierda).

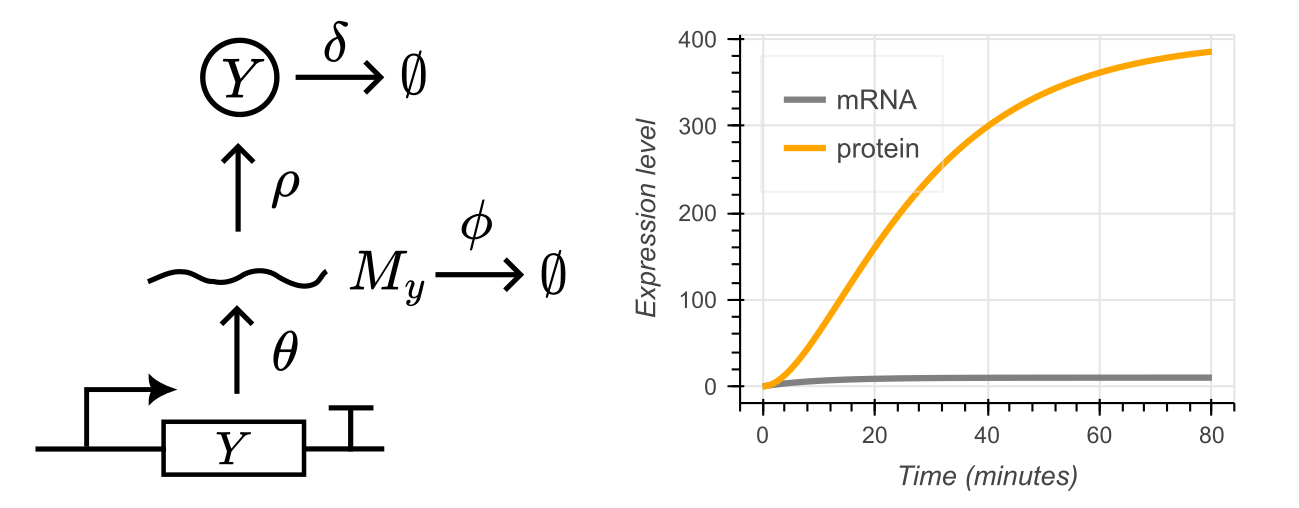
Podemos escribir las reacciones químicas, incluyendo la velocidad a la que ocurren estos eventos, como se muestra a continuación.

\begin{align} \text{DNA} &\xrightarrow{\theta} \text{DNA} + M_y && M_y \xrightarrow{\delta} \emptyset && \text{Transcription and degradation of mRNA}\\ M_y &\xrightarrow{\rho} M_y + Y && Y \xrightarrow{\phi} \emptyset && \text{Translation and degradation of protein} \end{align}

Podemos modelar cómo varía con el tiempo la concentración de las especies involucradas en estas reacciones utilizando Ecuaciones Diferenciales Ordinarias (ODEs) bajo la ley de acción de masas. Estas ODEs tienen la siguiente forma:

\begin{align} \frac{d}{dt} \text{species} = \text{production} - \text{degradation} \end{align}

Por lo tanto, modelamos nuestras reacciones químicas anteriores de la siguiente manera:

\begin{align} \frac{d}{dt} m_y &=& \theta - \delta m_y \\ \frac{d}{dt} y &=& \rho m_y - \phi y \end{align}

Como notación, usamos letras mayúsculas para referirnos a las especies químicas en sí (por ejemplo, $Y$, $M_y$), y letras minúsculas para referirnos a sus concentraciones (por ejemplo, $y = y(t)$ y $m_y = m_y(t)$). Si resolvemos el sistema de ODEs, podemos seguir cómo cambian estas concentraciones a lo largo del tiempo debido a las interacciones entre especies. Por ejemplo, en el lado derecho de la Figura 1, podemos ver cómo evolucionan las concentraciones de ARNm ($m_y$) y de proteína ($y$), basándonos en la solución numérica de nuestro modelo (ver Technical Note #1 para más detalles).

¿Qué es el estado estacionario?

Para algunos sistemas biológicos, incluyendo el que estamos estudiando aquí, si esperamos el tiempo suficiente, las reacciones alcanzarán un equilibrio cinético, donde las concentraciones de todas las especies dejan de cambiar con el tiempo. Esta condición se conoce como el estado estacionario. Podemos encontrar las concentraciones en estado estacionario igualando a cero el lado derecho de nuestras ecuaciones diferenciales y resolviendo las ecuaciones algebraicas resultantes. Utilizaremos una pequeña barra sobre la variable de la especie química para representar su valor en estado estacionario. Por ejemplo, $\bar{y}$ para representar el valor en estado estacionario de la variable $y(t)$.

En nuestro ejemplo, al resolver el estado estacionario del ARNm, obtenemos:

\begin{align} \bar m_y = \theta / \delta \end{align}

Ahora, al resolver el estado estacionario de la proteína $Y$, obtenemos:

\begin{align} \bar y = \frac{\rho}{\phi} \bar m_y = \frac{\rho}{\phi} \frac{\theta}{\delta} \end{align}

Si tomamos el valor en estado estacionario que acabamos de calcular y lo comparamos con la dinámica temporal de nuestras especies químicas (como se muestra en la Figura 1, derecha), podemos observar cómo las trayectorias se acercan gradualmente a ese valor a medida que pasa el tiempo.

Regulación génica a nivel transcripcional

Hicimos una suposición en nuestro modelo anterior: que la expresión génica está siempre ''activada''. Esto ocurre cuando el promotor que controla el gen es constitutivo, lo que significa que impulsa la expresión en todo momento, sin importar el contexto. Sin embargo, las células tienen una amplia variedad de mecanismos para decidir si un gen debe estar activo o no, dependiendo del entorno y de su estado interno. Una de las estrategias más comunes implica el uso de factores de transcripción. Estas son proteínas que reconocen una secuencia específica de ADN en el promotor, llamada sitio de unión. Cuando interactúan con ese sitio, pueden inhibir la expresión —como lo hacen los represores transcripcionales— o activarla, en el caso de los activadores transcripcionales.

La función de Hill se utiliza comúnmente para modelar la regulación mediada por factores de transcripción, y se basa en lo que se conoce como el argumento de separación de escalas de tiempo. La idea es que la unión entre un factor de transcripción y su sitio de unión en el ADN ocurre mucho más rápido que procesos como la transcripción y la traducción. Por lo tanto, si nos enfocamos en modelar los pasos más lentos, como la producción de ARNm y proteínas, podemos asumir que la unión del factor de transcripción alcanza su estado estacionario casi de forma instantánea. Esto simplifica el modelo, ya que no necesitamos seguir explícitamente la dinámica rápida.

Para modelar la regulación basada en factores de transcripción, utilizaremos la misma estructura del sistema TX-TL, pero ahora la proteína $Y$ puede inhibir o activar su propia expresión. Esto modifica la forma en que se regula la transcripción, ya que $Y$ ahora actúa como regulador de su propio promotor. Las reacciones químicas en este sistema se verán de la siguiente manera:

\begin{eqnarray} \emptyset &\xrightarrow{h(y)} M_y && M_y \xrightarrow{\delta} \emptyset && \text{Regulated transcription and degradation of mRNA}\\ M_y &\xrightarrow{\rho} M_y + Y && Y \xrightarrow{\phi} \emptyset && \text{Translation and degradation of protein} \end{eqnarray}

En este caso, $h(y)$ depende del tipo de factor de transcripción involucrado. Para un inhibidor, usamos $h(y) = \alpha \frac{K^m}{K^m + y^m}$, y para un activador, se convierte en $h(y) = \alpha \frac{y^m}{y^m + K^m}$.

En la Figura 2, podemos observar lo que se conoce como la curva de dosis-respuesta, la cual muestra la forma sigmoide característica de la función de Hill. Esta forma refleja cuán sensible es la expresión génica frente a cambios en la concentración del regulador. También podemos ver cómo la transición entre una expresión ''baja'' y ''alta'' se vuelve más pronunciada a medida que aumenta la cooperatividad ($m$ en las ecuaciones). Estas transiciones marcadamente abruptas se conocen como la propiedad de ultrasensibilidad.

Secuestramiento molecular

Otro tipo de regulación de la concentración de una especie química está dado por la reacción de secuestramiento molecular, que involucra a dos especies químicas, $Y$ y $Z$, que pueden unirse reversiblemente para formar un complejo $C$ que está inactivo. Esta reacción también se conoce como titulación estequiométrica, ya que una molécula 'secuestra' a otra en una relación 1:1 (Buchler & Louis, 2008.)

Una única reacción química está detrás de este proceso, y se puede escribir como:

\begin{eqnarray} Y + Z \overset{a}{\underset{d}{\leftrightarrows}} C \end{eqnarray}

donde $a$ se conoce como la tasa de asociación y $d$ como la tasa de disociación. Ahora usemos la ley de acción de masas para derivar las EDOs:

\begin{eqnarray} \frac{d}{dt}y &=& dc - ayz \\ \frac{d}{dt}z &=& dc - ayz \\ \frac{d}{dt}c &=& ayz - dc \end{eqnarray}

Si ''monitoreamos'' la concentración total de cualquiera de las especies $Y$ o $Z$, notaremos que estará disponible en dos estados en cualquier momento de la reacción: libre o unida (formando el complejo $C$). Entonces, si $y^T$ representa la concentración total de la especie $Y$, entonces $y^T = y + c$. Es un caso similar para la especie $Z$: $z^T = z + c$. Estas nuevas ecuaciones se conocen como las ecuaciones de conservación de masa.

Considerándolas, reescribamos la EDO para la especie $Y$ en nuestra reacción química.

\begin{eqnarray} \frac{d}{dt} y &=& d(y^T - y) - ay(y - y^T + z^T) \end{eqnarray}

Este es un polinomio de segundo orden que tiene dos soluciones. Sin embargo, una de ellas es negativa, lo cual no es viable ya que las concentraciones de especies químicas no pueden ser negativas. Por lo tanto, nos quedamos con una única solución (real y positiva):

\begin{eqnarray} \bar y = \frac{1}{2} \left [ (y^T - z^T - K) + \sqrt{(y^T - z^T - K)^2 + 4Ky^T} \right ] \end{eqnarray}

Para analizar el comportamiento de la especie $Y$, asumamos una afinidad muy fuerte entre las especies $Y$ y $Z$. Podemos modelar esta condición fijando $K$ a un valor muy pequeño.

En la Figura 3 (izquierda), podemos ver que cuando $z^T > y^T$, la salida es casi cero, ya que todas las moléculas de $Y$ son ''secuestradas'' por $Z$. Por otro lado, cuando $y^T > z^T$, la salida aumenta casi linealmente. Este comportamiento se conoce como thresholding. Si ahora observamos el mismo resultado en una escala logarítmica (Figura 3, derecha), podemos ver claramente una transición abrupta alrededor del punto umbral $y^T = z^T$. Este cambio pronunciado refleja la ultrasensibilidad del sistema cerca del umbral.

¿Qué tipo de operación matemática permite este mecanismo?

Al principio puede que no sea evidente, pero el secuestramiento molecular en realidad puede llevar a cabo una operación similar a una sustracción (o resta). Para entender mejor cómo esta pequeña reacción logra realizar ese cálculo, echemos un vistazo más detallado a los dos escenarios ilustrados en la Figura 4.

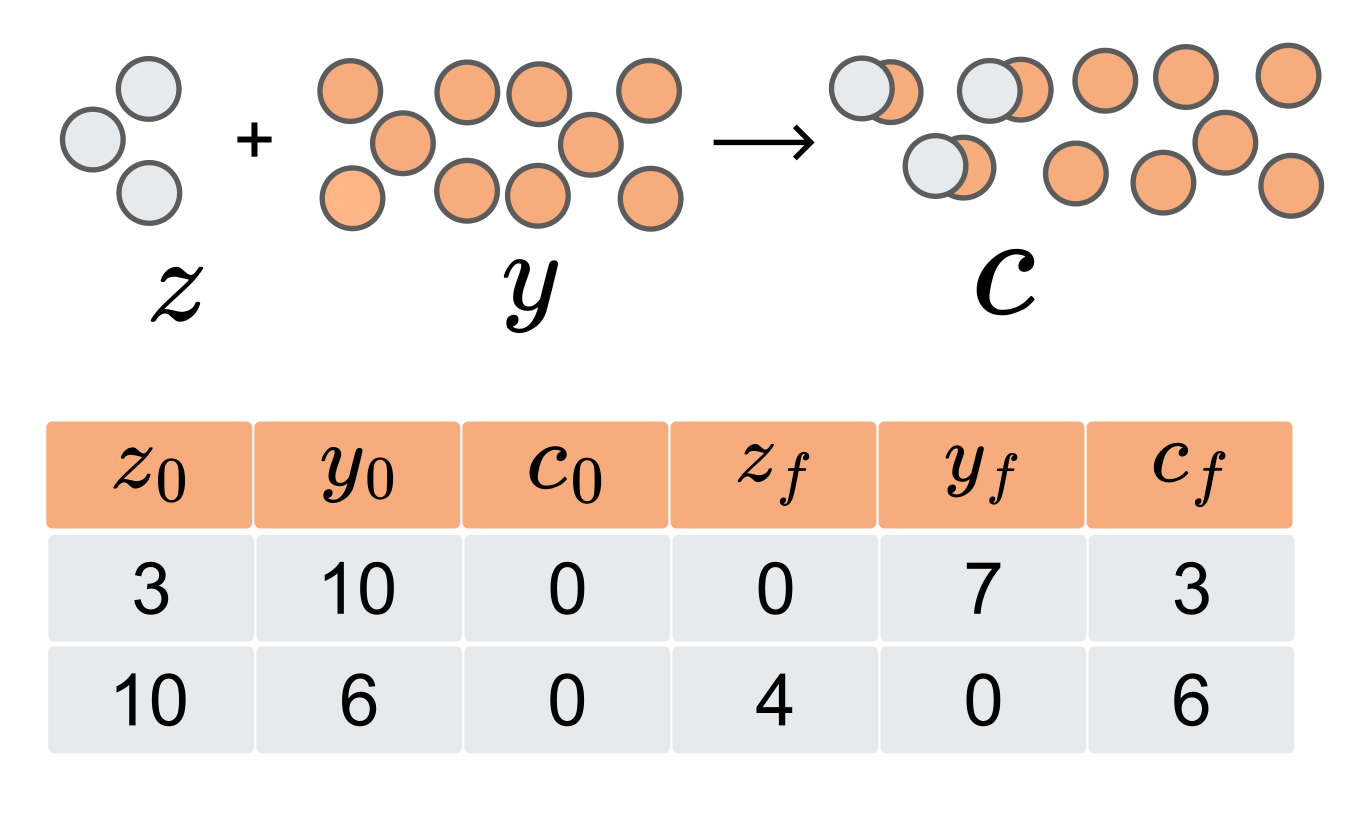
En todos los casos, comenzamos con una concentración inicial del complejo (denotado como $c_0$) igual a cero, ya que las especies $Z$ y $Y$ aún no han interactuado. Una vez que les permitimos unirse, la especie con la mayor concentración inicial termina secuestrando todas las moléculas de la que tiene menor concentración. En el primer caso, como $y_0 = 10$ y $z_0 = 3$, las tres moléculas de $Z$ forman complejos, y las siete moléculas restantes de $Y$ permanecen libres, lo que da como resultado $z_f = 0$, $y_f = 7$ y $c_f = 3$. En el segundo caso ocurre lo contrario: $z_0 = 10$ y $y_0 = 6$, así que las seis moléculas de $Y$ son secuestradas, y quedan cuatro moléculas de $Z$ sin unirse. Esto da como resultado $z_f = 4$, $y_f = 0$ y $c_f = 6$.

Sin entrar en una demostración matemática formal, podemos ver de forma intuitiva que la concentración final de cada especie sigue reglas simples. Para la especie $Y$, su cantidad final está dada por:

\begin{eqnarray} y_f = \max (0, y_0 - z_0) \end{eqnarray}

De forma similar, para la especie $Z$:

\begin{eqnarray} z_f = \max (0, z_0 - y_0) \end{eqnarray}

Finalmente, la concentración del complejo $C$, formado cuando $Y$ y $Z$ se unen, es simplemente el menor de los dos valores iniciales:

\begin{eqnarray} c_f = \min (y_0, z_0) \end{eqnarray}

Lecturas recomendadas

[1] Del Vecchio, D. and Murray, R.M. (2017) Biomolecular Feedback Systems. Princeton: Princeton University Press.

[2] Alon, U. (2020) An introduction to systems biology: Design principles of biological circuits. Boca Raton, FL: CRC Press.

[3] Grunberg, T.W. and Del Vecchio, D. (2020) ‘Modular analysis and design of Biological Circuits’, Current Opinion in Biotechnology, 63, pp. 41–47. doi:10.1016/j.copbio.2019.11.015.

[4] Samaniego, C.C. et al. (2023) ‘Building subtraction operators and controllers via molecular sequestration’, IEEE Control Systems Letters, 7, pp. 3361–3366. doi:10.1109/lcsys.2023.3294690.